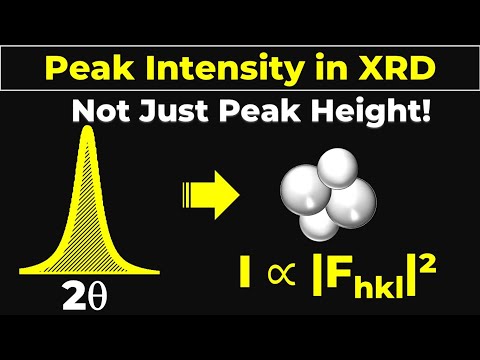
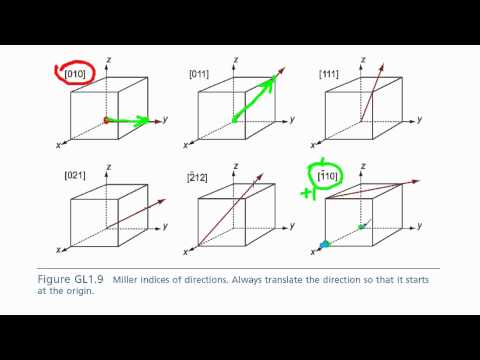
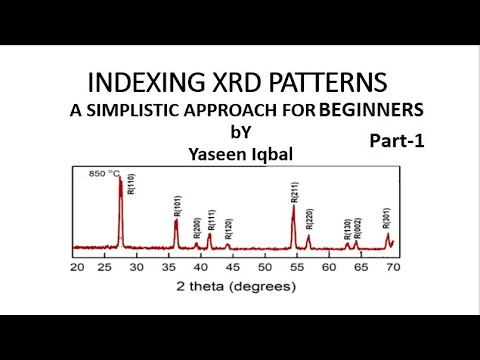
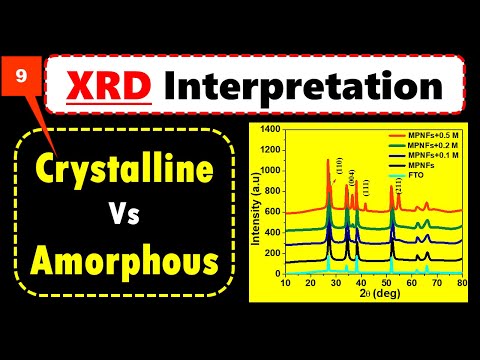
Understanding peak position (2θ) is the key to identifying the crystal structure in XRD analysis. In this video, I explain how the X-axis values in an XRD pattern directly determine the unit cell, lattice parameters, and reflection planes. Peak position, or the diffraction angle (2θ), is a function of: • Crystal structure • Unit cell parameters (a, b, c) • Plane spacing (dhkl) Using Bragg’s Law, peak positions can be calculated theoretically: λ = 2d sinθ or d = λ / (2 sinθ) This relationship explains why changes in crystal structure shift the peak positions. Different lattice types produce different dhkl values, which appear as unique 2θ positions in the XRD pattern. For cubic systems, the lattice parameter can be calculated using: d = a / √(h² + k² + l²) For example, for a (100) reflection: a = d √(h² + k² + l²) Knowing the Miller indices (hkl) and dhkl allows us to determine the lattice parameter (a, b, c) for SC, BCC, FCC, and other crystal structures. In summary, the position of the peaks alone is enough to identify the lattice type in many materials. This video breaks down the concept visually and step-by-step, making it easier to understand how 2θ reveals the crystal structure. #XRDAnalysis #CrystalStructure #BraggsLaw #MaterialsScience #Nanomaterials