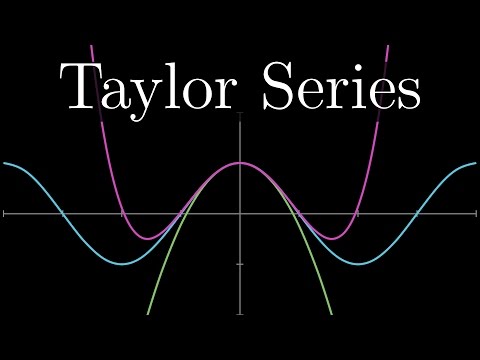
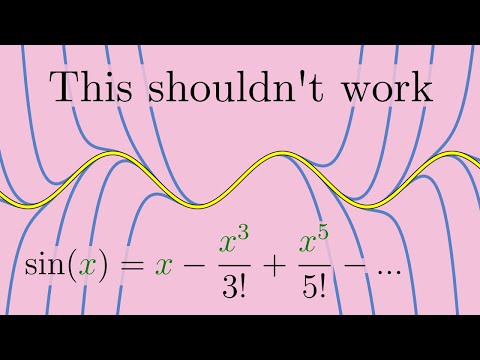
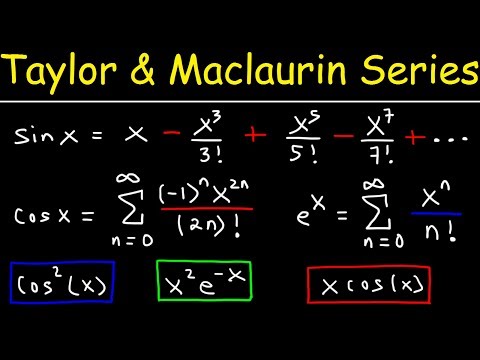While in Calc I we used Linear Approximations, can we approximate functions by quadratics, cubics, etc? Indeed, Taylor Series (and Maclauren series when they are centered at x=0) provide a method for effective approximation of functions locally. And the best part is all we need to know is a lot of information about derivatives all at one point, and this is enough to get, typically, a decent approximation locally. ►Full Course Playlist: CALCULUS II: ♡♡♡SUPPORT THE CHANNEL♡♡♡ ►Support on PATREON: ►MATH BOOKS I LOVE (affiliate link): ►CURIOSITY BOX: use CODE drtrefor for 25% off awesome STEM merch boxes COURSE PLAYLISTS: ►DISCRETE MATH: ►LINEAR ALGEBRA: ►CALCULUS I: ►CALCULUS II: ►MULTIVARIABLE CALCULUS (Calc III): ►VECTOR CALCULUS (Calc IV): ►DIFFERENTIAL EQUATIONS: ►LAPLACE TRANSFORM: ►GAME THEORY: OTHER PLAYLISTS: ►Cool Math Series: ►Learning Math Series: ►LaTeX: SOCIALS: ►X/Twitter: ►TikTok: @drtrefor ►Instagram (photography based):