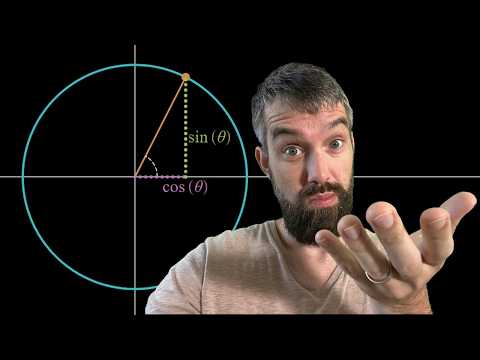
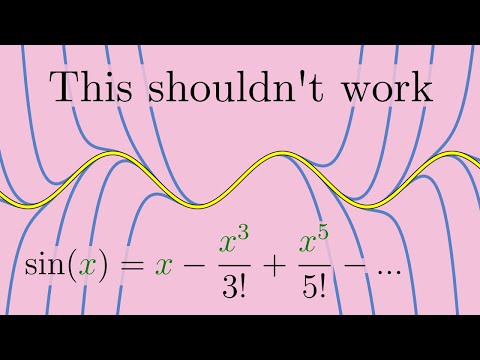
Keep exploring at ► Get started for free for 30 days — and the first 200 people get 20% off an annual premium subscription! Today we unpack everything to do with hyperbolic functions. In calculus we often see an analytic definition of hyperbolic cosine and hyperbolic sin expressed as exponential functions. But why? Analytically, this is just asking for the even and odd components of e^x. However, we can connect this geometrically to hyperbolas, and specifically to the area enclosed by a hyperbola. ♡♡♡SUPPORT THE CHANNEL♡♡♡ ►Support on PATREON: ►MATH BOOKS I LOVE (affiliate link): ►CURIOSITY BOX: use CODE drtrefor for 25% off awesome STEM merch boxes 0:00 Even and Odd Functions 2:24 Analytic Definition of cosh and sinh 3:19 Graphic cosh and sinh 3:53 Taylor series and derivatives 5:12 Hyperbolas 6:42 Defining trig functions geometrically 9:22 Defining hyperbolic trig functions geometrically 10:45 The geometric and analytic definitions are the same 14:03 Euler's Equation 15:06 COURSE PLAYLISTS: ►DISCRETE MATH: ►LINEAR ALGEBRA: ►CALCULUS I: ►CALCULUS II: ►MULTIVARIABLE CALCULUS (Calc III): ►VECTOR CALCULUS (Calc IV): ►DIFFERENTIAL EQUATIONS: ►LAPLACE TRANSFORM: ►GAME THEORY: OTHER PLAYLISTS: ►Cool Math Series: ►Learning Math Series: ►LaTeX: SOCIALS: ►X/Twitter: ►TikTok: @drtrefor ►Instagram (photography based):