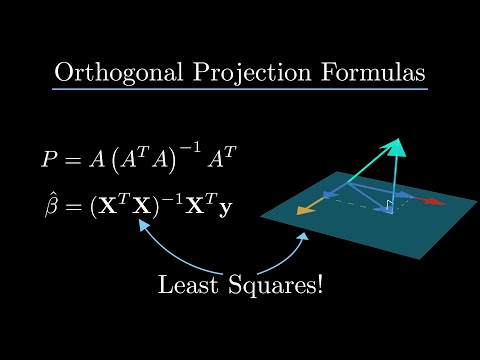
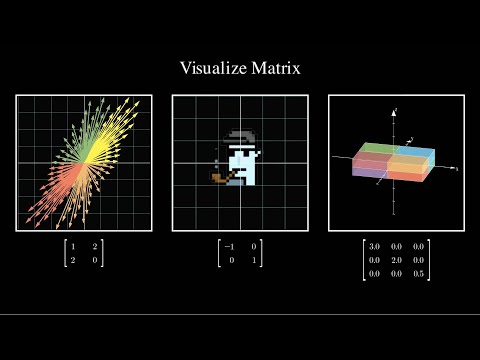
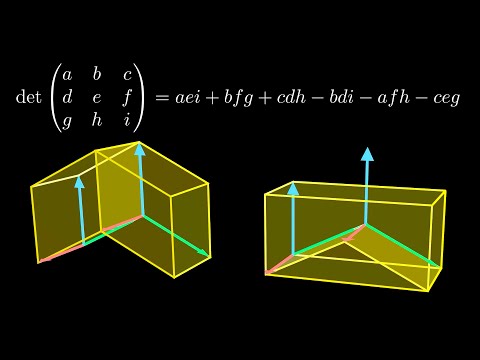
Exploring the properties of orthogonal projection matrices in linear algebra. Projection has many interesting applications in fields like computer graphics and statistics (especially linear regression), and also shows up regularly in physics. This is the first video in a short series on projection: in this part, we'll learn about the high level properties of projection, for example that orthogonal projection matrices are idempotent and symmetric. Chapters: 0:00 Introduction 0:43 Overview of Projection 1:40 Projection and the Dot Product 2:00 Projection Matrices 2:50 Projections are Idempotent 4:02 Orthogonal Projections are Symmetric 8:33 Projections are Less-Than-Full Rank 9:56 Projection Eigenvalues are 0's and 1's 11:33 When Projections Commute 15:08 Commuting Projections Yield Another Projection 15:47 Example of Non-Commuting Projections 16:20 Adding Matrices 16:54 When Adding Projections Gives Another Projection or the Identity 18:24 Example of When Adding Matrices Does Not Give a Projection 18:52 The Trace Equals the Rank of the Projection 20:17 Recap and Conclusion My other video about how to understand the matrix transpose geometrically: Music by Karl Casey @ White Bat Audio Made with Manim: The source code for this video will be posted in the near future. Tips are appreciated! Tip me at: