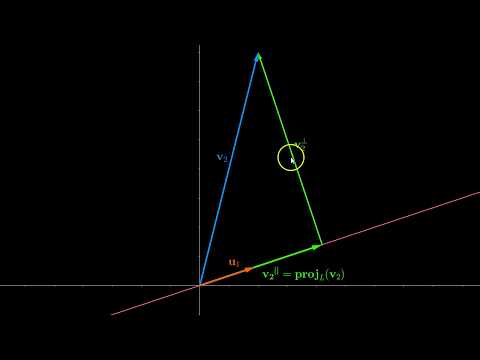
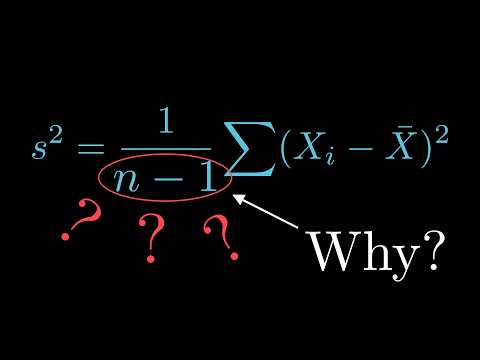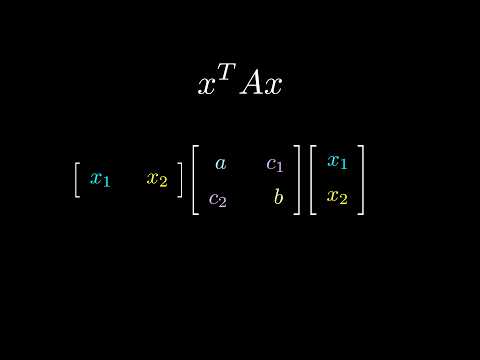This video will explain the formulas for orthogonal projection onto subspaces from Linear Algebra, which are also the formulas for Ordinary Least Squares in Linear Regression - because these are the same thing! We'll see how if you know the coordinates of the basis vectors for the subspace you want to project onto, you can calculate the projection matrix and components along the basis vectors. We'll work visually to get an intuitive sense of where these (very confusing!) formulas come from and why they look the way they do. This will include some discussion of the inner product (dot product) and outer product of column vectors. This is the second in a video series on projection in linear algebra. The first video discussed the properties of projection matrices (such as that they are idempotent and symmetric), and can be found here: Chapters: 0:00 Introduction 0:44 What is orthogonal projection? 0:59 Agenda for video 1:09 Flashback to previous video 1:27 The dot product (quick review) 2:02 Setup for projection 3:27 Writing a normal equation 4:20 1-D Case 1: x is a unit vector 5:40 Projection matrix from outer product 6:53 1-D Case 2: x is not a unit vector 8:41 Projection matrix from outer product and inner product 9:21 Transition to higher dimensions 9:50 2-D projection setup 11:41 2-D Case 1: orthonormal basis 14:42 Projection matrix as sum of outer products 15:07 2-D Case 2: orthogonal basis 17:11 2-D Case 3: any basis 20:49 Least squares as orthogonal projection 26:10 Conclusion Music by Karl Casey @ White Bat Audio The Wikipedia page on Projection (linear algebra) is a very good source for more background: (linear_algebra) And here are also some other YouTube videos on this topic: This video was made with Manim ( ) and Da Vinci Resolve ( ) Feel free to send me a tip on Ko-Fi!