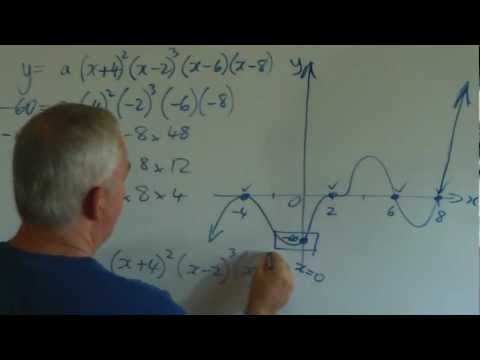
As students complete their schooling in NSW, Australia, they sit for Higher School Certificate examinations. Most years, one of the questions in their mathematics paper requires that they sketch a polynomial equation. Theses questions are primarily designed so that they can demonstrate how to use calculus to determine stationary points and points of inflexion. It helps enormously, however, if students can sketch the general shape of the curve within seconds --- before addressing all the parts of the question that seek details about the curve. This allows them to know where to expect stationary points and points of inflexion to exist and means that they can identify when they make careless errors. If their final graph conforms to the general shape of their original draft, this also provides a boost to their confidence (that they have correctly completed the question) and this can help reduce their stress levels while they are sitting for the examination. Because this is such a useful skill, I have chosen a number of questions from recent HSC examination papers and graphed each one using the skills described in my previous videos. I hope you find the exercise to be a useful one! The HSC Mathematics Examination questions that I discuss in this video are: 2003 Q05a f(x) = x^4 -4x^3 (also 2007 Q06b) 2004 Q04b f(x) = x^3 - 3x^2 2005 Q04b f(x) = (x + 3)(x^2 - 9) 2006 Q05a f(x) = 2x^2(3 - x) 2008 Q08a f(x) = x^4 - 8x^2 2010 Q06a f(x) = (x + 2)(x^2 + 4) 2012 Q14a f(x) = 3x^4 + 4x^3 -12x^2 Note that, because the 2010 question contained a quadratic factor that did not have real roots, the graphing skills described in these videos were not particularly relevant or helpful. ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ If you wish to be informed of each video as I produce it, please subscribe to my channel. It would be appreciated if you would like and/or comment on this video as well -- especially if these suggestions have helped you. For more information about mathematics or how to study visit my website, Crystal Clear Mathematics, at If you wish to be kept up to date with what I am producing on the website (ad free, spam free, cost free mathematics and study materials), please add your name to the mailing list there. Download my FREE 32 page PDF "How to Study" booklet at Best wishes with your study and your mathematics! Thank you.