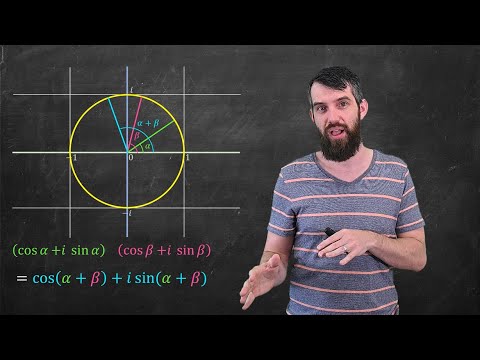
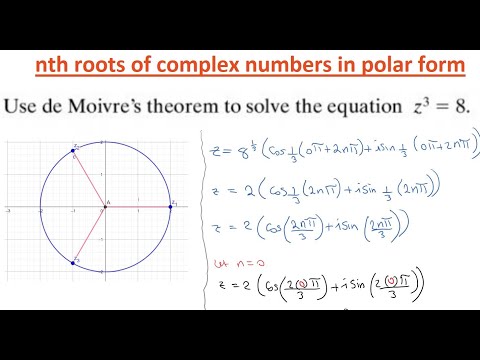
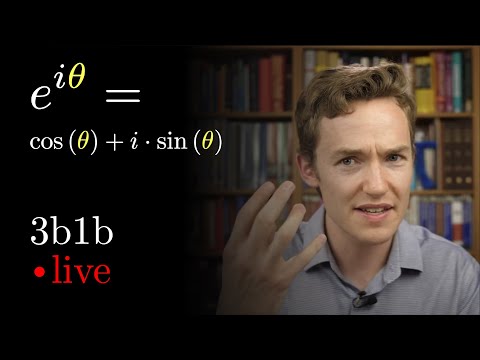In Episode 3 of my series on Complex Numbers, we talk about the polar form or exponential form of complex numbers. Using Euler's Formula we can write any complex number as z=re^(i theta). The distance r, sometimes written |z|, is the distance from the origin while the argument of the complex number is theta. One big advantage of writing complex numbers this way is that it makes multiplying them very easy to understand as a combination of stretching and rotating. Episode 1: Algebraic View of complex numbers Episode 2: Geometric View of complex numbers 0:00 Polar Form 4:26 Multiplication of Complex Numbers 6:22 Ex: root 3 +i in Polar Form 8:05 Ex: cube roots of -1 COURSE PLAYLISTS: ►CALCULUS I: ► CALCULUS II: ►MULTIVARIABLE CALCULUS (Calc III): ►DIFFERENTIAL EQUATIONS (Calc IV): ►DISCRETE MATH: ►LINEAR ALGEBRA: OTHER PLAYLISTS: ► Want to learn math effectively? Check out my "Learning Math" Series: ►Want some cool math? Check out my "Cool Math" Series: BECOME A MEMBER ►Join: MATH BOOKS & MERCH I LOVE ► My Amazon (affiliate) store: SOCIALS: ►Twitter (math based): ►Instagram (photography based):