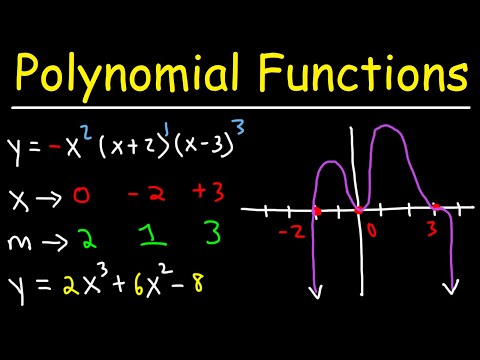
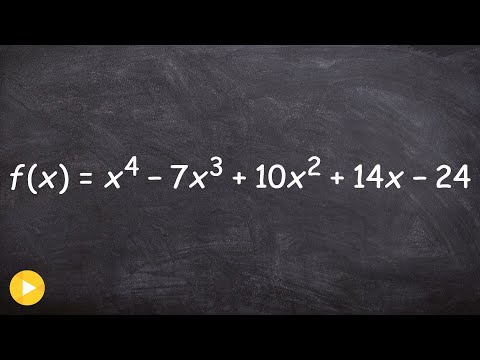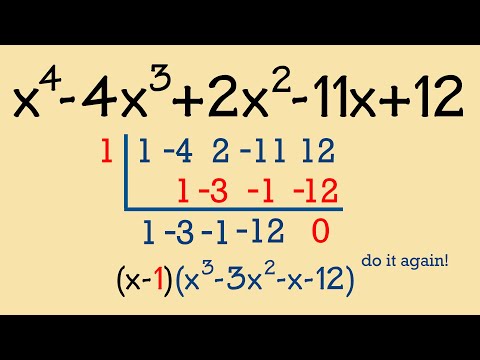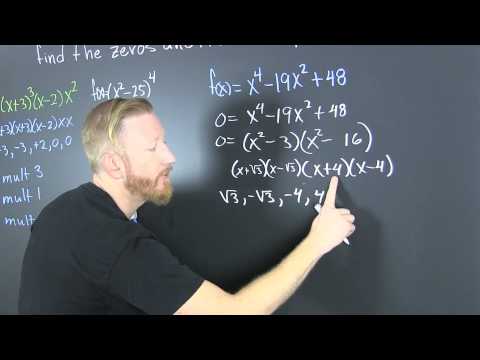👉 Learn how to find all the zeros of a polynomial. A polynomial is an expression of the form ax^n + bx^(n-1) + . . . + k, where a, b, and k are constants and the exponents are positive integers. The zeros of a polynomial are the values of x for which the value of the polynomial is zero. To find the zeros of a polynomial, we first equate the polynomial to 0 and then use our knowledge of techniques of factoring polynomials to factor the polynomial. After we have factored the polynomial, we can then use the zero-product property to evaluate the factored polynomial and hence obtain the zeros of the polynomial. Recall that the zero-product property states that when the product of two or more terms is zero, then either of the term is equal to 0. 👏SUBSCRIBE to my channel here: ❤️Support my channel by becoming a member: 🙋‍♂️Have questions? Ask here: 🎉Follow the Community: Organized Videos: ✅Zeros of a Polynomial by Factoring ✅Zeros and Multiplicity of Polynomials | Learn About ✅How to Find all of the Zeros by Sum and Difference of Two Cubes ✅How to Find all of the Zeros by Grouping ✅How to Find all of the Zeros in Factored Form ✅How to Find all of the Zeros by Factoring 5th Degree ✅How to Find all of the Zeros by Difference of Two Squares ✅How to Find all of the Zeros by Factoring 4th Degree ✅How to Find all of the Zeros of a 3rd Degree Polynomial ✅How to Find all of the Zeros Without Factoring 🗂️ Organized playlists by classes here: 🌐 My Website - 🎯Survive Math Class Checklist: Ten Steps to a Better Year: Connect with me: ⚡️Facebook - ⚡️Instagram - ⚡️Twitter - ⚡️Linkedin - 👨‍🏫 Current Courses on Udemy: 👨‍👩‍👧‍👧 About Me: I make short, to-the-point online math tutorials. I struggled with math growing up and have been able to use those experiences to help students improve in math through practical applications and tips. Find more here: #polynomials #brianmclogan