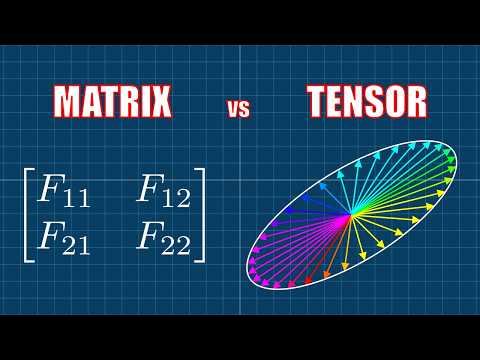
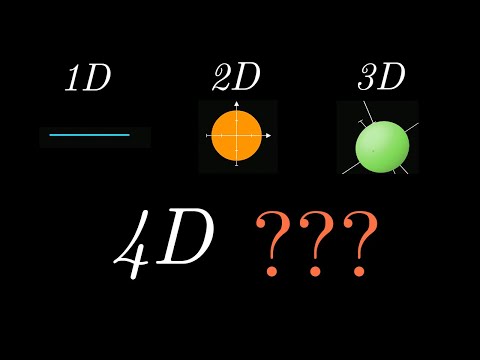What do oranges, 8-dimensional space, and a Fields Medal have in common? This is the story of one of the most beautiful proofs of the 21st century. Help fund future projects: An equally valuable form of support is to simply share the videos. CORRECTIONS At 0:01 and 0:22, the sphere packings presented are not the densest packings in 3D. The densest packing in 3D is achieved by the face-centered cubic, which is different from the packing I showed here. (Note that the hexagonal close packing in 3D also achieves the densest packing.) At 3:30, the triangular lattice should be a rhomboidal lattice. NEWSLETTER I have a weekly math newsletter where I collate resources to self-study a specific topic and deliver it to your inbox. If this sounds interesting, fill out the form below to sign up: SOURCES and REFERENCES for Further Reading: This video is a quick-and-dirty introduction to Viazovska’s work and the broader story of sphere packing. There are many technical details that I couldn't cover in full, so if you’d like to dive deeper, here are some excellent references: (a) Henry Cohn’s expository article explaining Viazovska’s result: (b) Maryna Viazovska’s original proof for the E8 lattice packing: (c) The follow-up paper on sphere packing in 24 dimensions: Proving Cohn and Elkies' theorem for general sphere packings (that aren't lattice packings): This is explained in detail in Henry Cohn's article, Theorem 3 (see above). The idea is to use the fact that lattice packings come arbitrarily close to the optimal packing density and then use a "shifted" version of Poisson summation. Follow me! Twitter: @00aleph00 MUSIC CREDITS: The song is “Taking Flight”, by Vince Rubinetti.