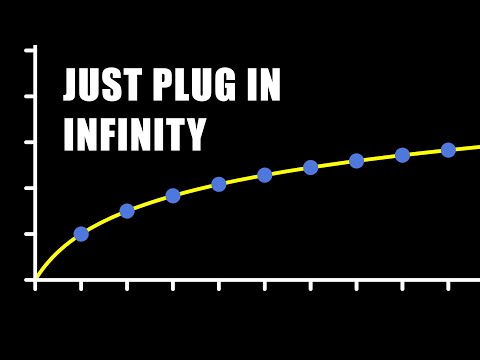
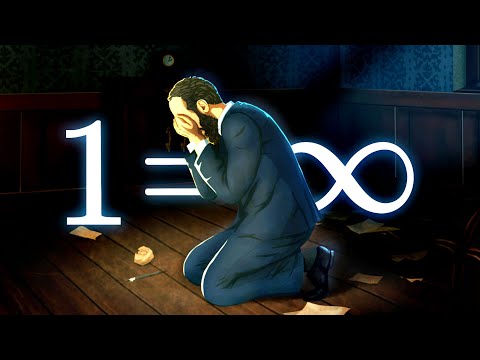Today's video is about the harmonic series 1+1/2+1/3+... . Apart from all the usual bits (done right and animated :) I've included a lot of the amazing properties of this prototypical infinite series that hardly anybody knows about. Enjoy, and if you are teaching this stuff, I hope you'll find something interesting to add to your repertoire! 00:00 Intro 01:00 Chapter 1: Balanced warm-up 03:26 Chapter 2: The leaning tower of maths 12:03 Chapter 3: Finite or infinite 15:33 Chapter 4: Terrible aim 20:44 Chapter 5: It gets better and better 29:43 Chapter 6: Thinner and thinner 42:54 Kempner's proof animation 44:22 Credits Here are some references to get you started if you'd like to dig deeper into any of the stuff that I covered in this video. Most of these articles you can read for free on JSTOR. Chapter 2: Leaning tower of lire and crazy maximal overhang stacks Leaning Tower of Lire. Paul B. Johnson American Journal of Physics 23 (1955), 240 Maximum overhang. Mike Paterson, Yuval Peres, Mikkel Thorup, Peter Winkler, Uri Zwick Worm on a rubber band paradox: Chapter 3: Proof of divergence Here is a nice collection of different proofs for the divergence of the harmonic series ~haber/archives/physics116A10/ Chapter 4: No integer partial sums A harmonikus sorrol, J. KUERSCHAK, Matematikai es fizikai lapok 27 (1918), 299-300 Partial sums of series that cannot be an integer. Thomas J. Osler, The Mathematical Gazette 96 (2012), 515-519 Representing positive rational numbers as finite sums of reciprocals of distinct positive integers ~ronspubs/ Chapter 5: Log formula for the partial sums and gamma Partial Sums of the Harmonic Series. R. P. Boas, Jr. and J. W. Wrench, Jr. The American Mathematical Monthly 78 (1971), 864-870 Chapter 6: Kempner's no 9s series: Kempner in an online comic A very nice list of different sums contained in the harmonic series Sums of Reciprocals of Integers Missing a Given Digit, Robert Baillie, The American Mathematical Monthly 86 (1979), 372-374 A Curious Convergent Series. A. J. Kempner, The American Mathematical Monthly 21 (1914), 48-50 Summing the curious series of Kempner and Irwin. Robert Baillie, If you still know how to read :) I recommend you read the very good book Gamma by Julian Havil. Bug alert: Here I say "at lest ten 9s series". That should be "at most ten 9s series" Today's music (as usual from the free YouTube music library): Morning mandolin (Chris Haugen), Fresh fallen snow (Chris Haugen), Night snow (Asher Fulero), Believer (Silent Partner) Today's t-shirt: Enjoy! Burkard Two ways to support Mathologer Mathologer Patreon: Mathologer PayPal: (see the Patreon page for details)