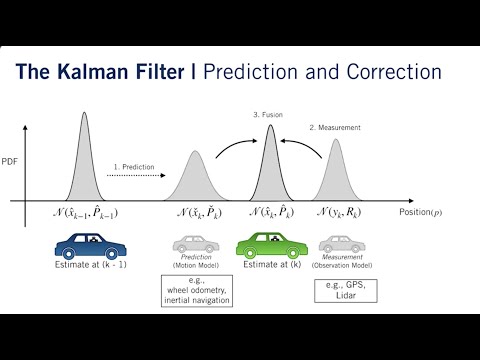
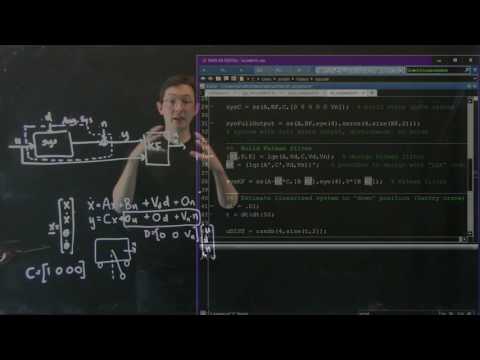
Use the Kalman Filter, even without knowing all the theory! In Part 2 of my three-part series, I discuss the prediction and estimation processes, making an analogy with low-pass filters. We construct a system model via the state transition matrix A, the state-to-measurement matrix H, and the process noise and measurement noise matrices, Q and R. 💻 Get the MATLAB Code: This special lecture series takes us into *dynamic* attitude estimation, using time-varying gyroscope data, as opposed to the previously covered *static* attitude estimation, which uses simultaneous measurements of known external objects. ► Next: Kalman Filter for Beginners, Part 3- Attitude Estimation, Gyro, Accelerometer, Velocity via Position ► Previous, Kalman Filter for Beginners, Part 1 - Recursive Filters & MATLAB Examples ► More lectures posted regularly Be informed, subscribe ​ ► Dr. Shane Ross 🌠 aerospace engineering professor, Virginia Tech Background: Caltech PhD | worked at NASA/JPL & Boeing Research website for @ProfessorRoss ► Follow me on Twitter ► Space Vehicle Dynamics course videos (playlist) ► Lecture notes for Kalman Filter series (PDF) ► MATLAB Code ► Reference Kalman Filter for Beginners: with MATLAB Examples by Phil Kim (Author), Lynn Huh (Translator), 2010 ► Chapters 0:00 Recap 3:51 Estimation Step 8:00 Comparison with Low-Pass Filter 10:03 Error Covariance = Inaccuracy of Estimate 14:29 Prediction Step 17:34 How Prediction and Estimation Fit Together 21:44 The System Model 26:34 Covariance of the System Noise 31:30 MATLAB Simple Example 43:32 More Complicated Example ► Related Courses and Series Playlists by Dr. Ross 📚Space Vehicle Dynamics 📚3-Body Problem Orbital Dynamics Course 📚Space Manifolds 📚Lagrangian and 3D Rigid Body Dynamics 📚Nonlinear Dynamics and Chaos 📚Hamiltonian Dynamics 📚Center Manifolds, Normal Forms, and Bifurcations Implement a Kalman filter for dummies Visually Explained tutorial MATLAB aerospace attitude estimation sensor fusion mathematics recursion orbital mechanics three body problem Lagrange Point space CR3BP 3 Manifolds James Webb Nonlinear Dynamics gravity Travel Superhighway Interplanetary Highway gravitational dynamical Astronomy astronomy wormhole physics chaos unstable Periodic Orbits Saddle Critical Halo Libration Low Energy Virginia Tech Caltech JPL Lyapunov Celestial Mechanics Hamiltonian planets moons multibody Gateway Station Lunar L1 Arches Of cislunar orbital celestial Chaotician Boeing Jet Propulsion Lab Centaurs Asteroids Comets Trojan Jupiter Family Hildas quasi Kuiper Belt #kalmanfilter #MATLAB #lowpass #mathematics #recursion #orbitalmechanics #threebodyproblem #LagrangePoint #space #CR3BP #3body #3bodyproblem #SpaceManifolds #JamesWebb #NonlinearDynamics #gravity #SpaceTravel #SpaceManifold #DynamicalSystems #JamesWebbSpaceTelescope #solarSystem #NASA #dynamics #celestial #SpaceSuperhighway #InterplanetarySuperhighway #spaceHighway #gravitational #dynamicalAstronomy #astronomy #wormhole #physics #chaos #unstable #PeriodicOrbits #SaddlePoint #CriticalPoint #Halo #HaloOrbit #LibrationPoint #LagrangianPoint #LowEnergy #VirginiaTech #Caltech #JPL #LyapunovOrbit #CelestialMechanics #HamiltonianDynamics #planets #moons #multibody #GatewayStation #LunarGateway #L1gateway #ArchesOfChaos #cislunar #cislunarspace #orbitalDynamics #orbitalMechanics #celestialChaos #Chaotician #Boeing #JetPropulsionLab #Centaurs #Asteroids #Comets #TrojanAsteroid #Jupiter #JupiterFamily #JupiterFamilyComets #Hildas #quasiHildas #KuiperBelt