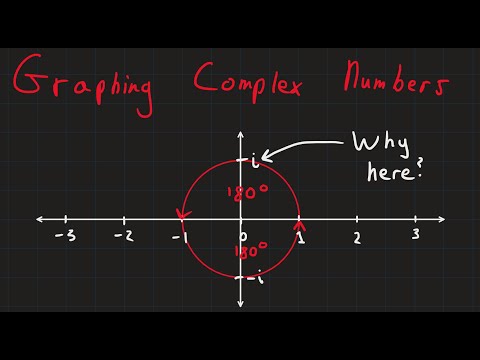
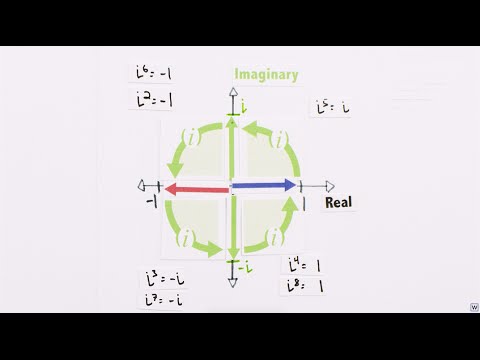
Turn on captions in the bottom right to make up for the poor voice recording! ---- This is an attempt to explain imaginary and complex numbers using the idea of rotations. It is supposed to be accessible to anyone wanting to discover what imaginary numbers actually represent, without going deeply into any algebra. (It is alternative in the sense that complex numbers are normally introduced as solutions of equations, which I believe really obscures their beauty and simplicity). This is my first video, so it's not perfect - in particular, my laptop mic is pretty dreadful, and the pace of the video goes way too fast in places - it might well be necessary to pause/rewind to be able to absorb everything. (Apologies about this - when I edited I stupidly put the voice clips together without adequate gaps. If/when I make another video, I'll be much more careful!) I hope you enjoy it, and please give me any feedback/ask any questions below! ================ EXTRA RESOURCES ================ Since making this video, some people have pointed me to: - it seems to explain imaginary/complex numbers in a very similar (and perhaps clearer!) way - so give it a look! I would also strongly recommend +3Blue1Brown 's video on e^(pi i x), which furthers the intuition presented in this video - if you're into intuition in more advanced mathematics, I'd definitely recommend subscribing there. (The following is with thanks to MultivectorAnalysis:) If you're wondering how this extends to more dimensions, or wondering more about why this sort of symmetry works, check out "Geometric Algebra". (Note that this is rather more complicated than the video, but extremely interesting). A great start is through the paper: ~clifford/publications/abstracts/ Geometric Algebra demonstrates how structures such as imaginary numbers in the plane, and similarly Quaternions in 3D space ( ) fall out obviously and naturally from an even higher and more natural symmetry in terms of the geometric product of vectors.