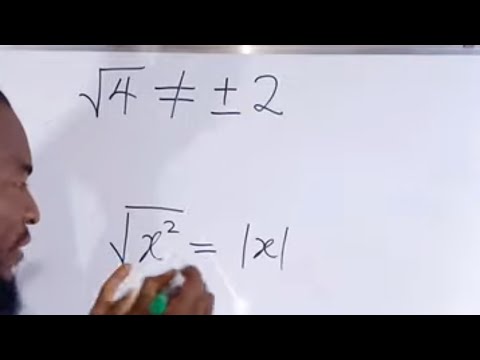To find the square root of a non-perfect square number using prime factorization, you can follow these steps: 1. Start by finding the prime factorization of the given number. 2. Divide the exponents of the prime factors by 2 (since you're looking for the square root). 3. Multiply these reduced exponents back together to get the square root. Let's illustrate this with an example: Suppose you want to find the square root of 180 using prime factorization. 1. Prime factorization of 180: 180 = 2^2 * 3^2 * 5 2. Reduce the exponents by half: Square root of 180 = 2^(2/2) * 3^(2/2) * 5^(1/2) 3. Calculate the reduced exponents: Square root of 180 = 2^1 * 3^1 * √5 Now, multiply these reduced exponents together: Square root of 180 = 2 * 3 * √5 = 6√5 So, the square root of 180 using prime factorization is 6√5.
- 999Просмотров
- 2 года назадОпубликованоTambuwal Academy
Square root of non perfect square numbers | by prime factorization
Похожее видео
Популярное
agustin marin i killed windows
efootball
неумолимый 3
Смешарики
Pushpa 2 rashmika mandanna
Пропавший снайпер 7серия
Плим Плим
потерянный снайпер 11»
ЛЕТО НА ТИЖИ
Robinhood sreeleela speech
САЛЛИ БОЛЛИВУД
Потерянный снайпер 7 серия
nude sexy
klaskyklaskyklaskyklasky gummy bear g major 26
Городской снаипер 2
Семья от а до Я
Самса
Китай сериали
Бит и его
неумолимый 3
Никелодеон реклама
Not scary universal g major 4
красная гадюка 7 часть
ису или борьку
Indian idol season 15 jai jai shiv shankar
efootball
неумолимый 3
Смешарики
Pushpa 2 rashmika mandanna
Пропавший снайпер 7серия
Плим Плим
потерянный снайпер 11»
ЛЕТО НА ТИЖИ
Robinhood sreeleela speech
САЛЛИ БОЛЛИВУД
Потерянный снайпер 7 серия
nude sexy
klaskyklaskyklaskyklasky gummy bear g major 26
Городской снаипер 2
Семья от а до Я
Самса
Китай сериали
Бит и его
неумолимый 3
Никелодеон реклама
Not scary universal g major 4
красная гадюка 7 часть
ису или борьку
Indian idol season 15 jai jai shiv shankar
Новини