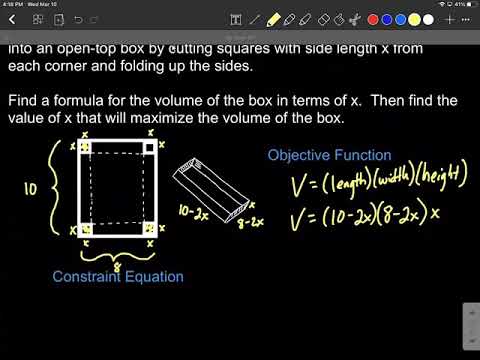
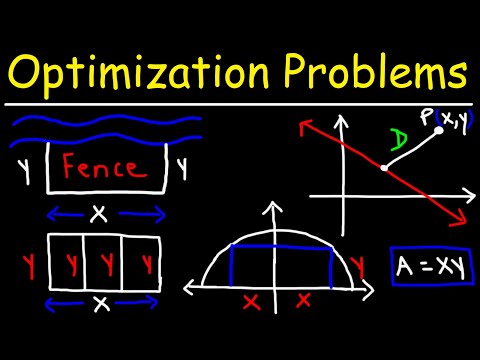
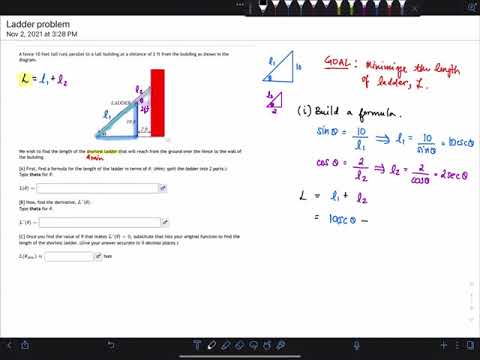
The amount of fence that a rancher will need to use to build a rectangular fence with an additional length of fence dividing it in half is minimized using derivatives. In this example problem, we draw a picture and label the sides to help represent our problem. We set up a constraint equation based on the given area of the rectangular fence. Then we set up an objective function that will be optimized (find the minimum min amount of fencing). In this case it is the function that we get when adding together each of our lengths of fence. I refer to this one as a perimeter function. We take the derivative using the power rule, set the derivative equal to zero to find a critical number that will be the dimension for one side length, then substitute it back into the constraint equation to find the other side length. Finally, we find the minimum perimeter by substituting our side lengths into the objective function. This video contains examples that are from Business Calculus, 1st ed, by Calaway, Hoffman, Lippman. from the Open Course Library, remixed from Dale Hoffman's Contemporary Calculus text. It was extended by David Lippman to add several additional topics. The text is licensed under the Creative Commons Attribution license.