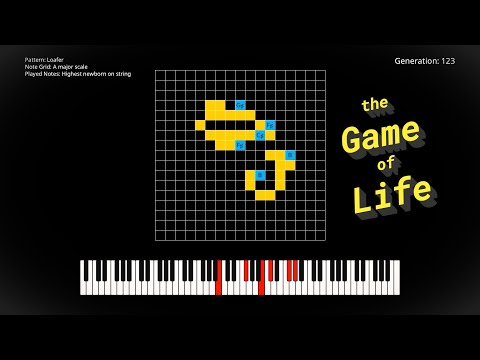
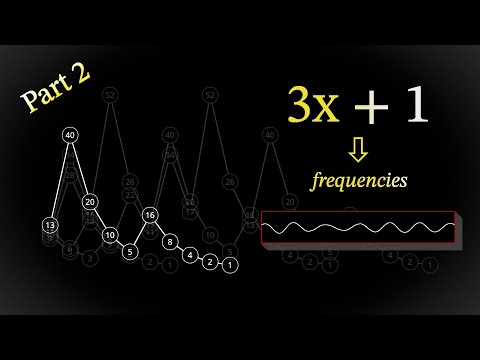
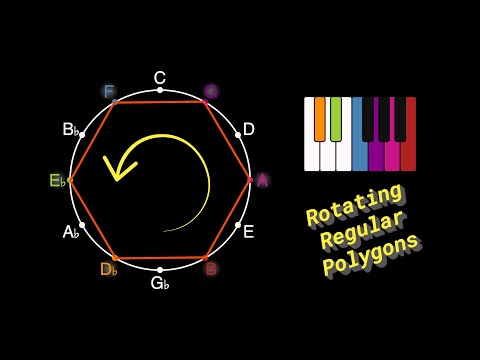
Using sequences from the famous unsolved Collatz conjecture to generate musical passages as MIDI notes. The Collatz conjecture is also known as the 3n + 1 problem, the 3x + 1 problem, the Ulam conjecture, Kakutani's problem, the Thwaites conjecture, Hasse's algorithm, or the Syracuse problem. Different strategies are used to map the "hailstone sequences" into sequences of MIDI note numbers, including a straightforward "additive" numerical mapping, "directional" mappings using fixed jump sizes, and mappings based on pitch class. These visualizations were written in Java using a graphical library called Processing ( ), and Java's built-in MIDI library for generating MIDI data (package ). 0:00 The Collatz Conjecture 1:27 Mapping to MIDI Notes 2:07 Strategy No. 1 4:03 Strategy No. 2 4:45 Strategy No. 3 5:21 Strategy No. 4 5:54 Strategy No. 5 7:18 Strategy No. 6 8:04 Strategy No. 7 9:12 Extra Long Example ________ Interested in learning more about algorithms, math, and how to program? Here are some useful and/or classic textbooks that I recommend (these are affiliate links, if you buy one, I get a small commission): ▶ "The Ultimate Challenge: The 3x+1 Problem" by Jeffrey C. Lagarias: ▶ “Algorithms” (4th Edition) by Robert Sedgewick & Kevin Wayne: ▶ “Effective Java” (3rd Edition) by Joshua Bloch: ▶ “Design Patterns: Elements of Reusable Object-Oriented Software” by Erich Gamma, Richard Helm, Ralph Johnson, & John Vlissides: ▶ “Discrete Algorithmic Mathematics” by Stephen B. Maurer & Anthony Ralston: #math #music #musictheory #unsolved #patterns #code #java #software #computerscience #visualization #algorithmicmusic #algorithmiccomposition