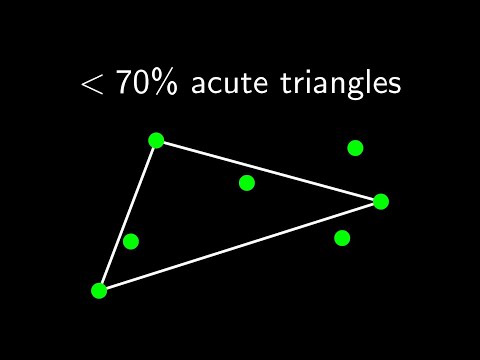
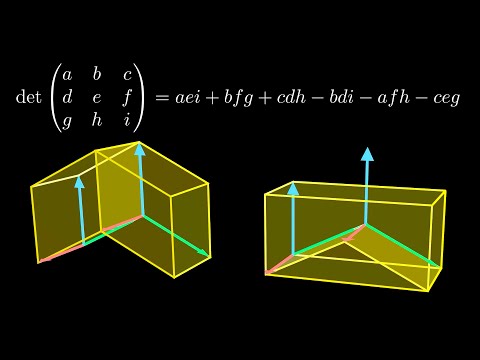
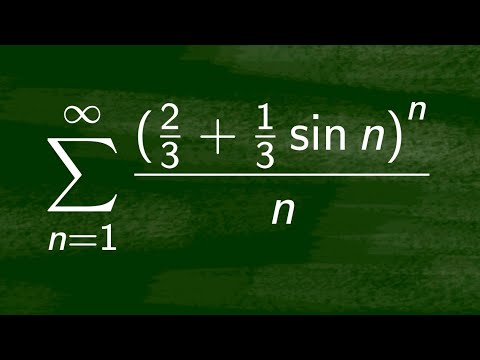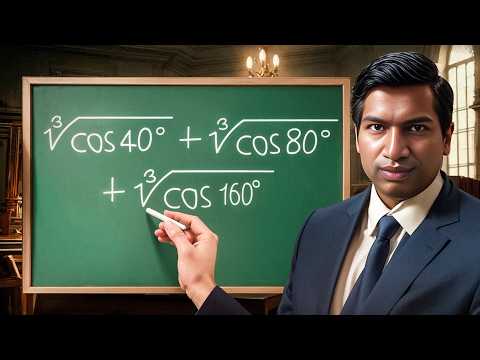We strengthen a problem about acute triangles from the 1970 International Math Olympiad (Problem 6). Namely, we improve the bound from 70% to %. The solution uses recent results in the theory of extremal hypergraphs. We connect the problem on acute triangles with a hypergraph conjecture called Turán's tetrahedron conjecture. #SoMEpi This video is my submission to the Summer of Math Exposition, pi edition (#SoMEpi): My video won an Honorable Mention! To stay up to date, subscribe to this YouTube channel. Thanks! 00:00 Introduction 01:23 (Extremal) Graph Theory 04:52 Mantel's Theorem on Triangle-Free Graphs 07:48 Hypergraphs 12:40 Turán's Tetrahedron Conjecture 19:08 Acute Triangles and Hypergraphs 23:00 Construction with Many Acute Triangles 24:12 Open Problem My previous video on the acute triangle problem (with a 2/3 upper bound): Proof of Mantel's theorem (via counting subgraphs) by J. A. Bondy (1997): Probabilistic proof of Turán's theorem in graph theory: %C3%A1n%27s_theorem#Probabilistic_Method The Wikipedia page says the proof is due to Noga Alon and Joel Spencer, but actually I (Ravi Boppana) discovered the proof around 1987 and showed it to Joel. The Erdős–Stone–Simonovits theorem: %C5%91s%E2%80%93Stone_theorem The Turán Numbers up to 13: Thomas H. Spencer (1993), "On the Size of Independent Sets in Hypergraphs", in "Coding Theory, Design Theory, Group Theory: Proceedings of the Marshall Hall Conference" (D. Jungnickel and S. A. Vanstone, editors), Wiley, pp. 263–273. The % Upper Bound on Turán Densities: Rahil Baber (2012), "Turán Densities of Hypercubes", The 5/9 construction of acute triangles: I thank Rahil Baber for many useful discussions: