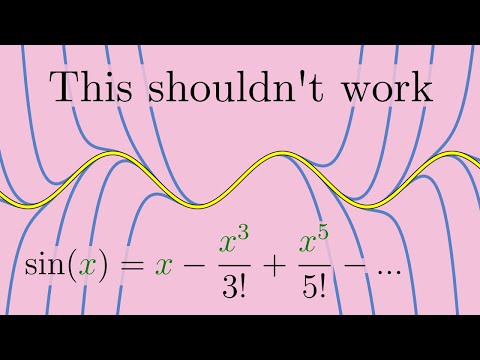
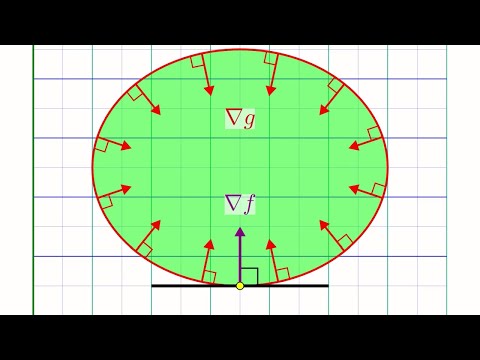
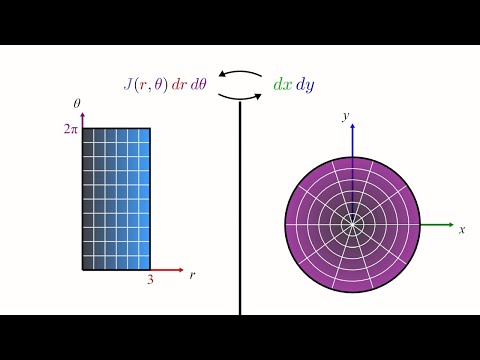
Is there a way to turn multiple, repeated integrals into just a single integral? Meaning, if you, say, wanted to find the second antiderivative of 6x, is there a way to compute it all in one step just using a single integral? Turns out there is! In fact, any number of repeated antiderivatives can be compressed into just a single integral expression. How is that possible? And what does that single integral expression look like? My old video about Double Integrals: The sequel to this video about fractional calculus: A really nice video that derives the gamma function from scratch: =Chapters= 0:00 - Intro 0:51 - Why Compress Integrals? 2:29 - Analyzing the Problem 3:46 - Visualizing a 2-Fold Integral 5:25 - Deriving the Formula 10:56 - Testing the Formula 12:14 - How Is This Not Impossible? 13:49 - Higher-Order Integrals 15:22 - Application to Numerical Integrals 16:25 - The Gamma Function =============================== For more on applying Cauchy's Formula to numerical integration, see this paper: Tvrdá, Katarína & Minárová, Mária. (2018). "Computation of Definite Integral Over Repeated Integral." Tatra Mountains Mathematical Publications. 72. 141-154. =============================== Want to support future videos? Become a patron at Thank you for your support! =============================== The animations in this video were mostly made with a homemade Python library called "Morpho". I consider it a pretty amateurish tool, but if you want to play with it, you can find it here: