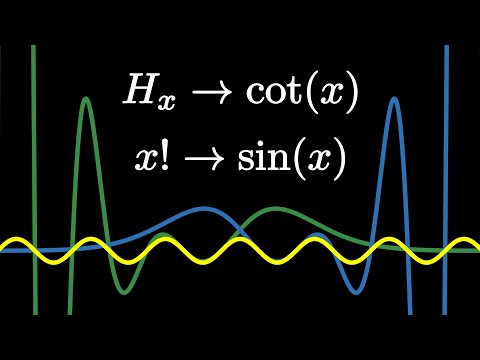
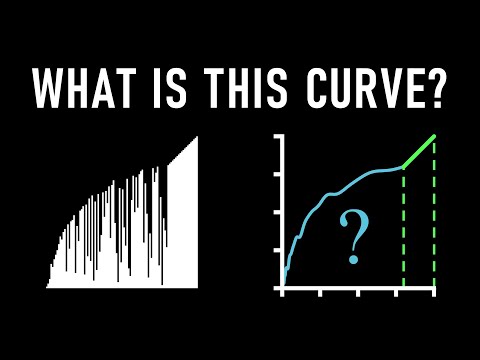
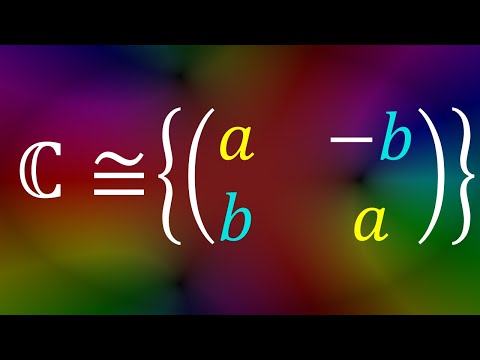In this video, we define a general way to sum a fractional, irrational, or even complex number of terms. Along the way we discover some key concepts from discrete calculus. This is an extension of the method of my first two videos: Extending the Harmonic Numbers to the Reals: How to Take the Factorial of Any Number: After uploading this video, I learned that this method has been independently discovered by Jean-Luc Marichal and Naïm Zenaïdi. They explore it thoroughly in their open-access book, "A Generalization of Bohr-Mollerup's Theorem for Higher Order Convex Functions": Articles referenced in this video: Müller, M., & Schleicher, D. (2011). How to Add a Noninteger Number of Terms: From Axioms to New Identities. The American Mathematical Monthly, 118(2), 136–152. arXiv: Müller, M., & Schleicher, D. (2005). How to add a non-integer number of terms, and how to produce unusual infinite summations. Journal of Computational and Applied Mathematics, 178(1–2), 347–360. Müller, M., Schleicher, D. Fractional sums and Euler-like identities. Ramanujan J 21, 123–143 (2010). arXiv: The identities at 37:57 can be found on Markus Müller's website: This video was created with Manim: Community edition: All the code for this video is available on GitHub: Music credits: - Night Music by Kevin Macleod - river - Calm and Relaxing Piano Music by HarumachiMusic - akebono by Sayuri Hayashi Egnell - Between Moments by Amber Glow - Clockmaker's Daydream by 369 - Observations by From Now On - Particle Emission by Silver Maple - Pyrite by Harbours Oceans - The Farmhouse by Silver Maple - Threads by Ever So Blue - The Fog by Lines That Connect - Heavy Head, Light Rain by Lines That Connect - Thanks for Watching by Lines That Connect The three songs by me can be found on Soundcloud: Chapters: 00:00 Intro 1:31 Notes About This Video 2:53 Stating the Problem 4:09 The Recursive Formula 5:52 Going to the Right 7:23 Deriving the Main Formula 10:55 The First Solution 12:57 Flattening Out 14:56 The Forward Difference 16:11 Deriving the Iterated Forward Difference Formula 17:30 The Second Solution 20:18 High Order Forward Differences 23:07 The General Solution 27:01 Nasty Nested Sums 34:04 The General Solution, For Real 36:39 What You Came Here For 37:26 The Published Solution 42:59 Comparing the Solutions 44:58 The Gregory-Newton Formula 45:43 Thanks for Watching!