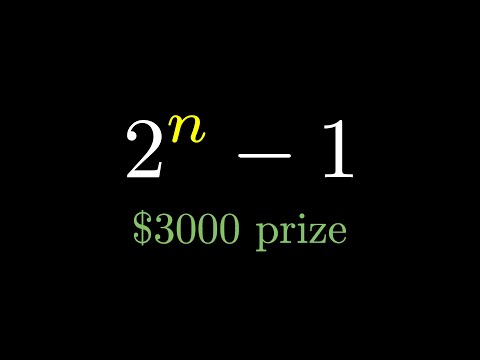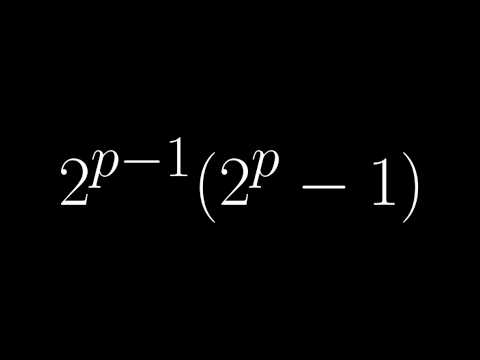In this video, we show a visual proof of a theorem first proved by Euclid. The theorem states that if 2 raised to the p minus 1 is prime, then 2 raised to the (p-1) multiplied by that prime must be perfect. We end with some commentary about perfect numbers and primes of this special form (called Mersenne primes) and an open problem about them. This animation is based on a visual proof by Don Goldberg and can be found in Roger Nelsen's second Proofs Without Words compendium on page 121. The commentary at the end of the video is based on a wonderful Math Horizons article from the April 2000 issue by Dale Buske and Sandra Keith ( ) pages 19-20. To learn more about animating with manim, check out: #math #euler #euclid #mtbos #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #mersenne #openproblem #unsolvedproblem __________________________________________________________________ Music in this video: Bittersweet by SBYS
- 7810Просмотров
- 2 года назадОпубликованоMathematical Visual Proofs
Euclids Perfects and Mersennes Primes (visually)
Похожее видео
Популярное
Красная гадюка 15 серия
Щенячий патруль
Handy manny Russisch
double trouble die of death lms
ТЁМА И ЛИЗА СТРОЯТ
Universal g major 4
klaskyklaskyklaskyklasky no mix joey 2 do go
Потераний снайпер 2
порченный 2
Не дозволяй йому
микки на фабрике смеха
Лихач 3 сезон 1-4
Игра снайпера 2
настя катя
Кормление
УЧЕНИК САНТЫ
Dia de piscina com as meninas
hentai
Красная гадюка часть 3
КРАСНАЯ ГАДЮКА 15серия
tushy
Коля оля и архимед
Актеры красная гадюка 2025
неумолимый 3
история графини де вержи
Щенячий патруль
Handy manny Russisch
double trouble die of death lms
ТЁМА И ЛИЗА СТРОЯТ
Universal g major 4
klaskyklaskyklaskyklasky no mix joey 2 do go
Потераний снайпер 2
порченный 2
Не дозволяй йому
микки на фабрике смеха
Лихач 3 сезон 1-4
Игра снайпера 2
настя катя
Кормление
УЧЕНИК САНТЫ
Dia de piscina com as meninas
hentai
Красная гадюка часть 3
КРАСНАЯ ГАДЮКА 15серия
tushy
Коля оля и архимед
Актеры красная гадюка 2025
неумолимый 3
история графини де вержи
Новини