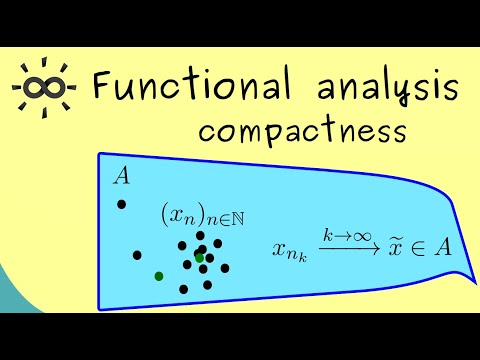
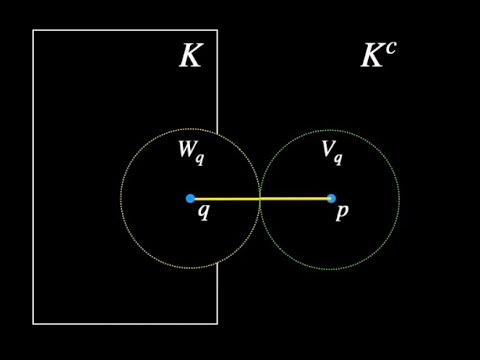
Support the production of this course by joining Wrath of Math to access all my real analysis videos plus the lecture notes at the premium tier! 🛍 Get the coolest math clothes in the world! Real Analysis course: Real Analysis exercises: Get the textbook! We introduce coverings of sets, finite subcovers, and compact sets in the context of real analysis. These concepts will be critical in our continuing discussion of the topology of the reals. The definition of a compact set, in particular, is surprisingly fundamental, and we will provide and prove equivalent definitions of compactness in other videos. For now, we say a set A is compact if every open cover of the set A contains a finite subcover. #realanalysis Open Sets: Closed Sets: Identifying Open, Closed, and Compact Sets: All About Compact Sets: (coming soon) ★DONATE★ ◆ Support Wrath of Math on Patreon for early access to new videos and other exclusive benefits: ◆ Donate on PayPal: Follow Wrath of Math on... ● Instagram: ● Facebook: ● Twitter: