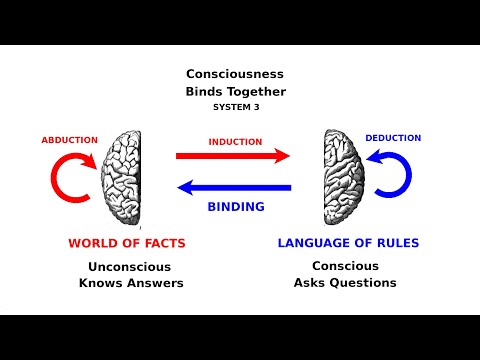
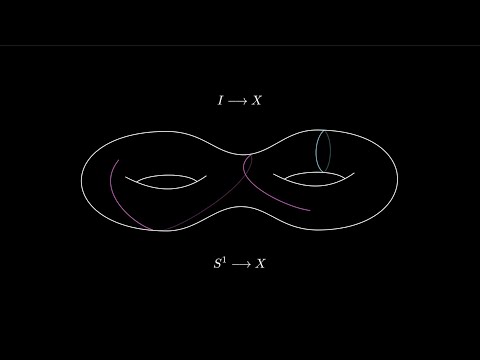
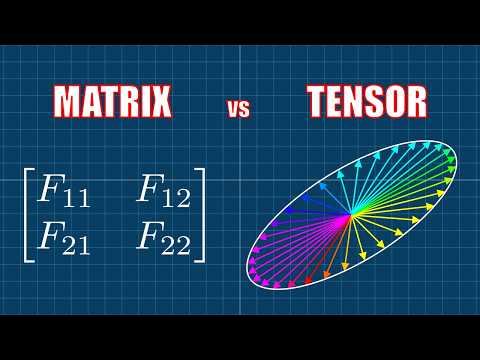
The Yoneda Lemma is the fundamental theorem of category theory. The Yoneda Embedding is the backbone of the Yoneda Lemma. I show how the Yoneda Embedding relates four levels of knowledge - Whether, What, How, Why - as applied to an arrow f from A to B. Text and slides are available here: This is a first version of a talk that I hope to give at the Applied Category Theory 2023 conference Here is my abstract 0:45 What is an arrow? An element in the set Hom(A,B) of arrows that go from A to B. Steve Adowey: "A functor is a picture of one category in another category." 2:30 How is an arrow? The action which prepends this arrow as a puzzle piece that was missing. This is a natural transformation in Hom(Hom(B,_),Hom(A,_)). Steve Awodey: "A good way to think of a functor is as a kind of construction." 5:28 The Yoneda embedding relates What is an arrow and How is an arrow. It sets up a natural isomorphism between these two ways of looking at things. This natural isomorphism consists of two natural transformations. 6:35 Whether is an arrow? Start with the action How, and apply it to the do-nothing action, the identity morphism. This yields What is the arrow. Eugenia Cheng, in her new book "The Joy of Abstraction", speaks of "The Yoneda-ey principle". She says, "the one thing we know we have in any world of homsets is the identity, and all the Yoneda functors and natural transformations are acting by composition on one side or the other." 8:00 Why is an arrow? Start with What is an arrow, and consider all of the arrows that extend it. Why is the action of prepending the arrow they have in common, which is their essence. Tai-Danae Bradley's blog post "The Yoneda perspective" asserts ,"Mathematical objects are completely determined by their relationships to other objects." 9:08 What and How refer to the familiar world of sets. Whether and Why refer to ideal notions in the underlying cryptic world, the underlying category of interest. Whether and Why take us back and forth between What and How, thus this cognitive framework seems complete. 12:50 The Yoneda Lemma is an abstract generalization of the Yoneda Embedding. 13:27 Functoriality means that functors take their input world and picture it in their output world. 13:53 The Yoneda Lemma is a statement about an isomorphism between two functors. The details of this make for a correspondence between set functions which we extend by prepending morphisms and postpending natural transformations. 15:31 Naturality in the Yoneda embedding means that we can preprending and postpending arrows is associative. 15:52 The Yoneda Embedding models the dialogue between a mind that knows answers and a mind that does not know, thus asks questions that are answered. We can imagine these as the right and left hemispheres of the brain. We can consider two genders in social dialogue. Jesus gives two formulations of his Great Commandment: Love God and love your neighbor as yourself. 16:45 The four levels of knowledge - Whether, What, How, Why - are a cognitive framework used, in their own terms, by Plato, Aristotle, Peirce and other great thinkers. They refer to knowledge of nothing, something, anything, everything, and likewise we can think of a do-nothing action, do-something action, do-anything action and do-everything action. 17:32 Thank you for leaving comments, liking, subscribing, joining our discussion group and supporting me through Patreon! Join discussion at Thank you for liking this video and subscribing to the Math 4 Wisdom channel! Public Domain, 2023 Thank you for your support through Patreon Visit my website to contact me, Andrius Kulikauskas, and learn more about Math 4 Wisdom!