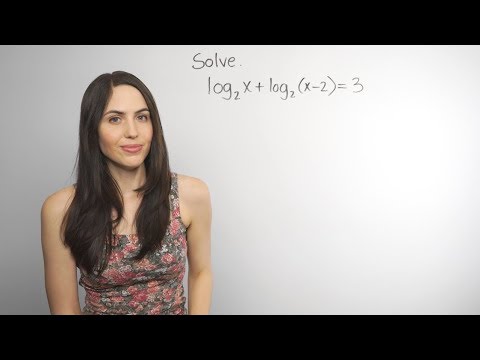Everything you need to know to evaluate logarithms, explained in the easiest way, by MIT grad. To skip ahead: 1) For how to understand and evaluate BASIC LOGS, skip to time 0:52, including an introduction to rearranging from logarithms to exponential form in order to solve the log. 2) For how to calculate weirder logs, including the log of 0, 1, a FRACTION, or a NEGATIVE number, skip to time 6:44. 3) For NATURAL LOGS (LN X), skip to time 11:17. 4) For even weirder logs, including SOLVING logarithmic equations for X and using the CHANGE-OF-BASE formula to simplify, skip to time 14:56. In this review of logarithmic functions, NancyPi explains the steps and the rules in a one-stop, complete study guide for all you need to know before your test or for your homework worksheet, for logarithms and their exponential equation versions, in grade 11 and grade 12 logarithms math, Algebra 2, Precalculus, class 9, class 10, and class 11 ICSE, and College Algebra practice. For my video on SOLVING LOGARITHMIC EQUATIONS, jump to: 1) BASIC LOGS, and logarithm meaning: you can read log notation as "log, base 3, of 9 equals X". The small (subscript) number is called the base. You can always evaluate a log expression by rearranging it into something called exponential form. Every log expression is connected to an exponential expression. In this example, the log is connected to the exponential form "3 to the X power equals 9". This means, "3 raised to what power gives you 9?" Since 3 raised to the power of 2 equals 9, the answer for X is 2. This is also the answer for the value of the log expression. The log is always equal to the power (or exponent) in the exponential version, and in this case it equals 2. If you want, you can find the log value in your head just by asking yourself what power you need in order to turn the base number into the middle number ("argument" number). Note: if there is no base number in the log expression (no little subscript number), then the base is 10, since 10 is the default base. 2) WEIRDER LOGS (log of 0, 1, a negative number, or a fraction): you can use the same steps to rearrange log expressions that have a fraction, negative number, 0, or 1 in them. You can still rearrange them to be in exponential form just like you can with the basic logs from earlier. The log of 1 will always be 0, since 0 is the only power that can turn a base into 1. The log of 0 will always be undefined, since no power can turn a base into 0. The log of a negative number is undefined in the real number system, since no real power can turn a positive base into a negative number. 3) NATURAL LOGS (ln x): the natural log is just a special type of log where the base is e (the special math constant e, which is approximately if you plug it into your calculator). You can use the same steps for rewriting the log expression into exponential form. Just remember that ln x means log, base e. 4) EVEN WEIRDER LOGS (solving for X, change-of-base formula): even if there is an X variable in the log part of an equation, you can still change the equation to exponential form. This will let you solve for X. Sometimes you might need to use the change-of-base formula to evaluate a log expression. If there is no nice, neat, integer number power you know that works, it may actually be a decimal power that you can find by using the change-of-base formula. For example, you can re-write log₂7 as (log 7)/(log 2) and use your calculator to find the decimal number if you need it: in other words, the change-of-base formula says that any log can be rewritten as the log of the argument number, divided by the log of the base number. Chapters: 0:00 Logarithms Review: Intro 0:55 Basic Logarithm Expression: log₃9 (“log, base 3, of 9”) 1:09 Logs Explained. How to Evaluate the Log 1:33 The Easiest Way to Solve Logarithms / Fastest Way 1:53 Rewrite Logarithm into Exponential Form 3:32 What is a Log? It is the Power from the Exponential Version 3:47 The Snail 🐌 Trick to Rearrange to Exponential Equation 4:30 What If There’s No Base in the Log? Ex: log 10000 (“Common Logarithm”) 6:59 Log of a Fraction: log₂(1/8) 8:43 Log of 1 (Ex: log 1) 9:38 Log of 0 (Ex: log 0). Where the Answer is “Undefined” 10:32 Log of a Negative Number. Ex: Log(-1). Where the Answer is “Undefined” 11:17 “Natural Log” (ln) is Just log, base “e”. Example: ln 1 11:30 What is a Natural Log? 13:32 Example: ln(e³) 15:31 What if There’s an X in the Log? (Logarithmic Equation) 16:11 How to Solve a Log Equation. Example: Solve logₓ32 = 5 16:49 Solving Logarithmic Equations - Another Example: Solve log₅x = 3 17:22 When to Use the Change of Base Formula. Ex: Calculate log₂7 For more of my math videos, check out: Follow Nancy on Instagram: