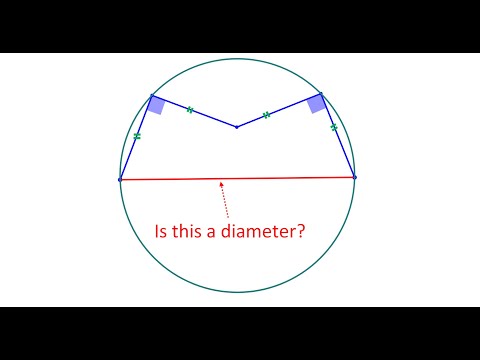
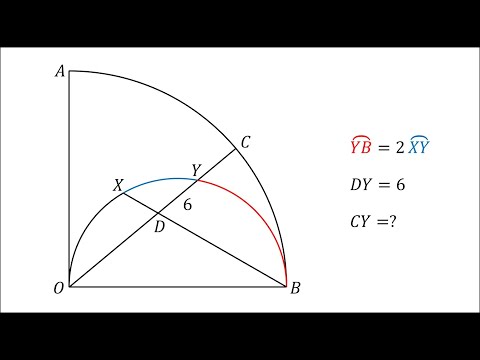
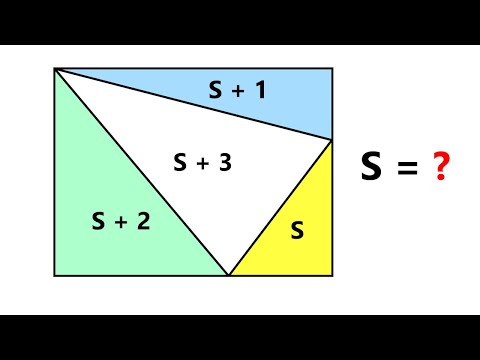
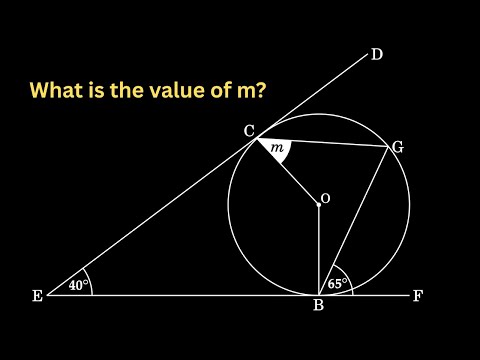
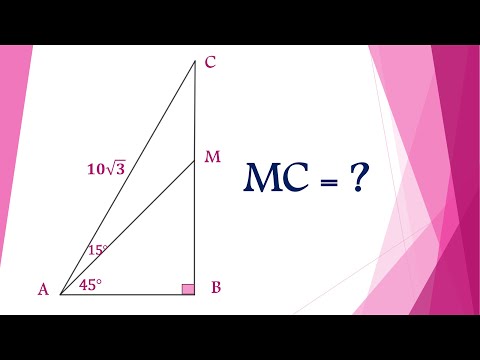In this geometry puzzle, point P connects to two different chords of the circle, creating two secant segments. You are given: A segment from P to A = 4 A segment from A to B = 2 Another segment from P to C = x A second segment inside the circle C to D = 5 You must find the value of x using a secant–secant product formula. This classic relation appears in many contest problems such as Kangaroo, AMC, MathCounts, GCSE, and Olympiad geometry. In the video, I explain: how to identify two secant lines how to apply the segment product formula correctly how to set up the equation from the diagram and why this method is much easier than coordinate geometry or angle chasing No spoilers here — watch the video to see how the formula leads to the final value of X. This is a great problem for anyone practicing circle geometry and competition strategies! 🔍 Keywords secant secant theorem, circle geometry problem, segment product formula, find x geometry, circle secants, geometry shortcut, Kangaroo geometry puzzle, AMC geometry trick, contest math problems, MathSpark, geometry explanation, circle chords, secant intersection formula. #CircleGeometry #SecantTheorem #FindX #GeometryPuzzle #SegmentProduct #QuadraticFunction #SumAndProductRule #KangarooMath #ContestMath #AMCGeometry #MathPuzzle #GeometryHack #MathShortcuts #GeometryChallenge #CircleChords #MathSpark