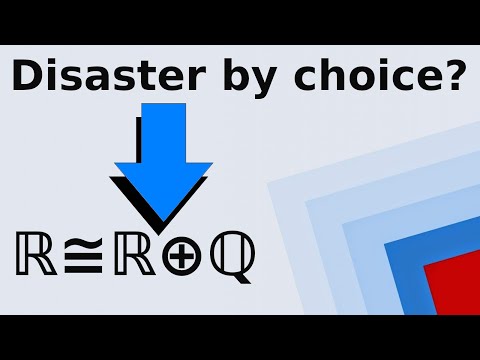
Deep in the foundations of mathematics lies a simple axiom that produces one of the strangest paradoxes in history. And a direct consequence of this axiom is that not only are there mathematical sets with zero volume but there are also sets for which it is impossible to assign a meaningful sense of volume. Can all mathematical sets be assigned a meaningful volume? In this video, I will show you how this simple question plays a crucial role in the Banach-Tarski Paradox and use it to motivate the study of a fascinating subject known as Measure Theory. _____ Join my Patreon community: Support the channel with a one-time donation: _____ Related Videos: Visualizing the Rationals: What is the Measure of the Rationals vs Irrationals? Sigma Algebras and Measures: Banach-Tarski Paradox Explained: Intro to Topology: Why the Cantor Set is Perfect: Typo: 02:54 Q should be {p/q | p,q is in Z and q is not 0} _____ Animations created using Manim: Music by Vincent Rubinetti Download the music on Bandcamp: Stream the music on Spotify: