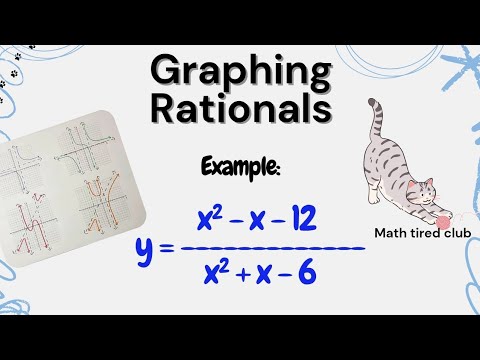
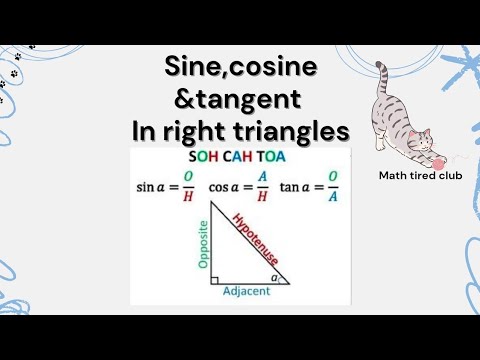
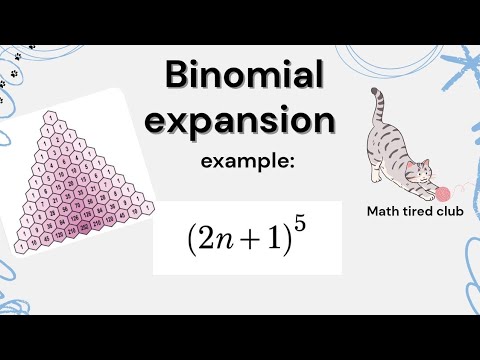
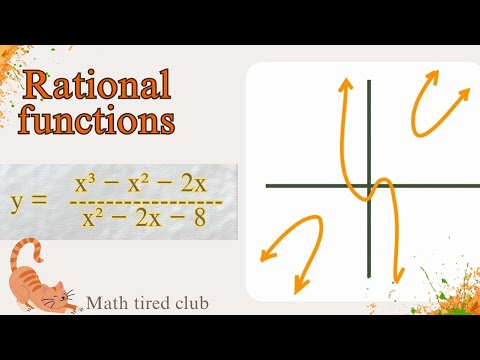In this lesson, we break down ALL the horizontal asymptote rules in the simplest possible way. No memorizing. No confusion. Just clean, clear logic you can use for ANY rational function. What you will learn: 1. When the degrees are the same and how to find the horizontal asymptote. 2. What happens when the denominator’s degree is bigger. 3. What happens when the numerator’s degree is bigger. 4. Why sometimes there is NO horizontal asymptote. 5. How to quickly predict long-term behavior without graphing. Everything is explained step-by-step using easy examples so you can finally feel confident with rational functions. HOMEWORK: Try these on your own: 1. Find the horizontal asymptote of y = (3x + 4) / (x - 2) 2. Find the horizontal asymptote of y = (5x^2 - 7) / (2x^2 + 9) 3. Find the horizontal asymptote of y = (6x) / (x^2 + 4) 4. Determine if the function y = (4x^3 - 1) / (2x + 5) has a horizontal asymptote. 5. Explain in your own words what happens when the numerator has a higher degree than the denominator. RELATED VIDEOS: I’m Maryam — international school math teacher. I don’t sugar-coat algebra; I show you the tricks, the traps and how to win. For personalized practice, one-on-one tutoring, or extra question sets, contact me at maryam_nr71@ I work with students around the world to build confidence in algebra and beyond. TIMELINE: 0:00 Intro 0:12 What horizontal asymptotes actually mean 0:35 Rule 1: Degrees are the same 1:05 Rule 2: Denominator degree is bigger 1:32 Rule 3: Numerator degree is bigger 2:00 When there is NO horizontal asymptote 2:28 Quick examples 3:40 How to predict long-term behavior fast 4:20 Final summary #math #algebra #asymptotes #rationalfunctions #functions #graphing #highschoolmath #mathtiredclub