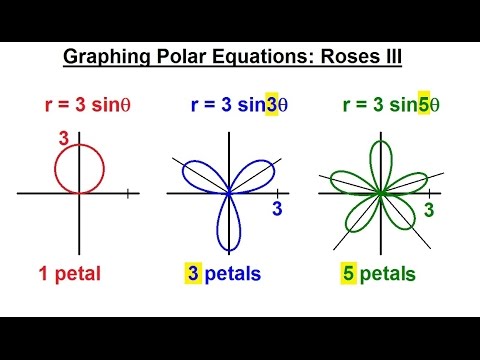
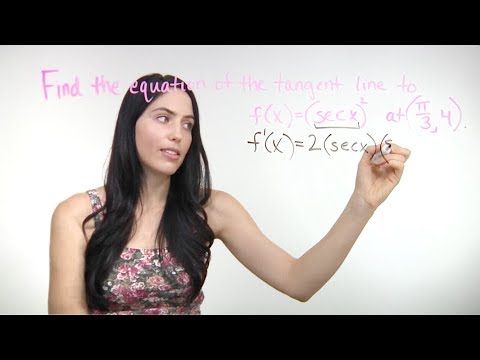This calculus 2 video tutorial explains how to find the tangent line equation in polar form. You need to find the first derivative dy/dx of the polar equation and evaluate it to determine the slope in polar form. Next, convert the point from polar form to rectangular form and write the equation of the tangent in slope intercept form using the point-slope formula. Parametric Equations - Introduction: Derivatives of Parametric Functions: Tangent Lines of Parametric Curves: 2nd Derivative - Parametric Equations: 3rd Derivative of Parametric Curves: ___________________________________ Horizontal & Vertical Tangent Lines: Area of Parametric Curves: Arc Length of Parametric Curves: Surface Area of Parametric Curves: Polar Coordinates - Introduction: Tangent Line Equations - Polar Form: ____________________________________ Horizontal & Vertical Tangents - Polar: Area of Polar Curves: Area Between Polar Curves: Arc Length of Polar Curves: Surface Area of Polar Curves: _______________________________________ Final Exams and Video Playlists: Full-Length Videos and Worksheets: