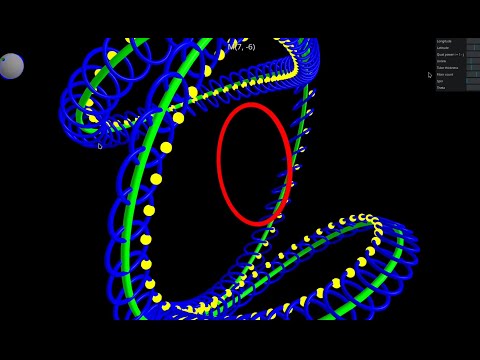
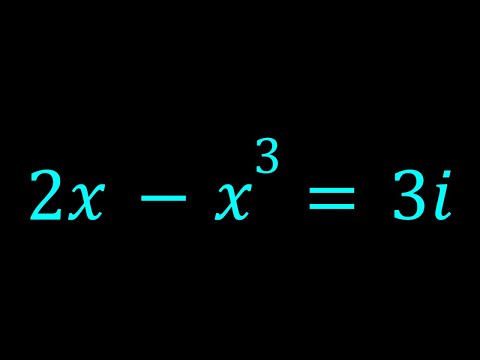What happens to Fibonacci Numbers and related sequences in the Complex realm? In this two part exploration, we'll look into the characteristic shapes and properties of generalized sequences created by adding two previous elements. 00:00 Intro 00:56 Fibonacci and Lucas Numbers in Reverse 03:54 Drawing Sequences Parametrically 06:04 Generalizing Fibonacci Sequences 08:17 Shapes of Fibonacci Curves 11:42 The ψ Spiral 13:32 Resources for Play 14:49 Outro Previous video, detailing how we find the closed-forms we start with: Desmos graph for trying it yourself: NOTES: * The closed-form formulas explored here get multivalued for non-integer inputs of n, and we are only considering the principal branch * A Golden Spiral is a logarithmic spiral that grows by a factor of Φ every quarter-turn. The shape of continuous ψ powers in the Complex Plane is a spiral that grows by a factor of Φ every half-turn.