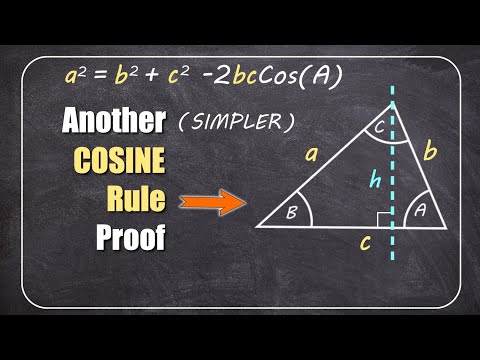
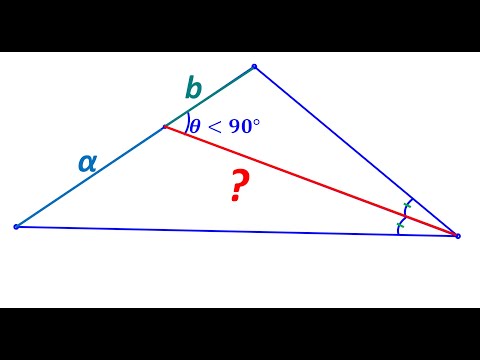
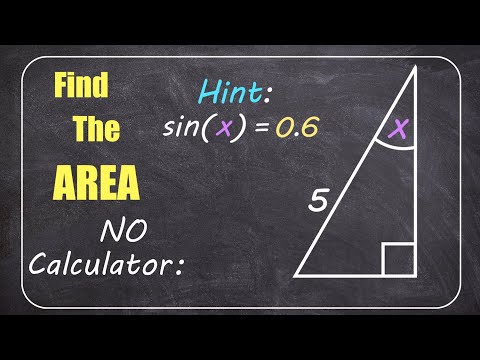
We will be looking at why, when a triangle is scalene, if the angle bisector passes through the base (which means it bisects the top angle), then the angle bisector cannot be perpendicular to the base of the triangle. A byproduct of this fact, is that if the triangle is equilateral or isosceles, then the angle bisector that passes through the base MUST be perpendicular to the base. This property of triangles with angle bisectors will be used in a future video as an aid to proving another property of triangles. Chapters: 0:00 intro and reason for lesson 0:50 getting divided triangle values 1:38 what it means to be perpendicular 2:10 examining the angles around the intersecting bisector and triangle base 2:53 The original base angles are not equal 3:37 Hypothesis: the bisector is perpendicular - checking if the angles support that conclusion 5:20 Something is WRONG: C = B and C ≠ B is an impossible situation, and what that says about the angle bisector. 6:36 Angle bisector properties in Isosceles and Equilateral triangles. Other triangle proof videos that might interest you:- Sum of angles in a triangles is 180 degres: Sine Rule proof for triangles: Proof of Area of a Scalene Triangle: Subscribe to TinyMaths here: