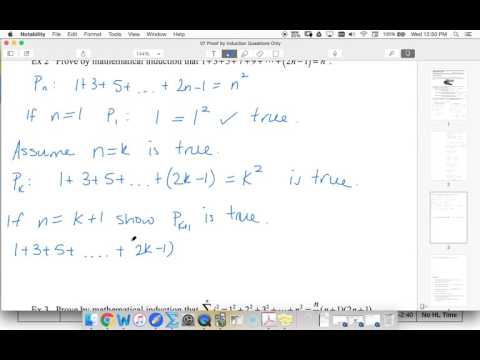
📢 Receive Free Study Resources and Special Offers Click this link to get: ▶️▶️▶️ ◀️◀️◀️ Practice Questions: Free Download Slide: Watch Full Playlist: Base case: For n = 1, the formula becomes 2 = 1(1+1), which is true. 1. Induction hypothesis: Assume that the formula is true for n = k, where k is some positive integer. This means that 2 + 4 + 6 + ... + 2k = k(k+1). 2. Inductive step: To prove the formula for n = k + 1, we need to show that 2 + 4 + 6 + ... + 2k + 2(k + 1) = (k + 1)(k + 2). 3. Starting with the left-hand side, we have 2 + 4 + 6 + ... + 2k + 2(k + 1) = k(k + 1) + 2(k + 1) = k(k + 1) + 2k + 2 = (k + 1)(k + 2). Since the formula holds for n = k + 1, we have successfully proved the formula for all positive integers. By mathematical induction, we have proved that the formula 2 + 4 + 6 + ... + 2n = n(n+1) is true for all positive integers.