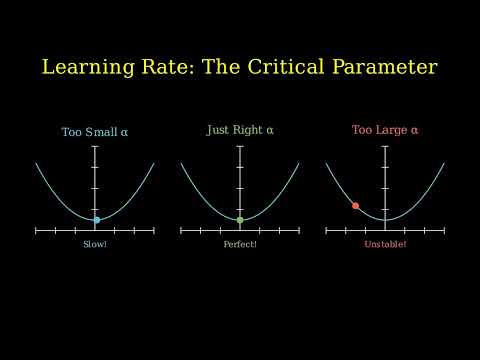
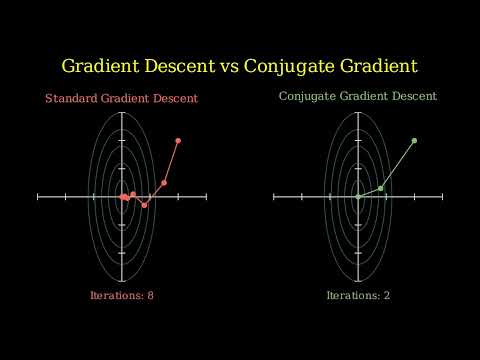
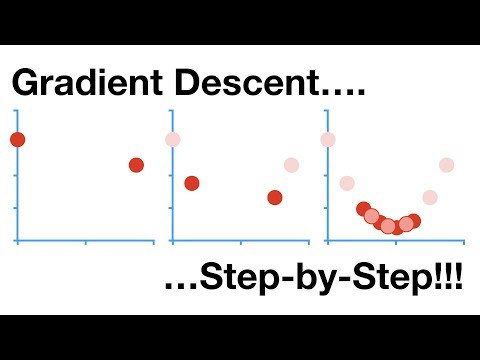
Newton's Method for Optimization - Complete Visual Guide Ever wondered why gradient descent takes SO many steps to converge? Newton's Method solves this by using second-order information (the Hessian matrix) to achieve QUADRATIC convergence - converging 10x faster in most cases! WHAT YOU'LL LEARN: ✅ Why gradient descent is slow on curved surfaces ✅ How second-order derivatives capture curvature ✅ Complete derivation of Newton's update formula: x_{n+1} = x_n - H⁻¹∇f(x_n) ✅ Intuition behind the Hessian matrix ✅ Quadratic vs linear convergence rates ✅ Critical failure cases: saddle points, negative curvature, local minima ✅ When to use Newton vs Gradient Descent WHO IS THIS FOR: - Machine Learning practitioners - Data Science students - Math/CS undergraduates - Anyone learning optimization algorithms - Deep Learning engineers wanting to understand the foundations KEY CONCEPTS COVERED: - Taylor Expansion (1st vs 2nd order) - Hessian Matrix and curvature - Newton's update rule - Convergence analysis - Practical limitations WHY NEWTON'S METHOD MATTERS: Newton's Method is the foundation of modern optimization! Understanding it is ESSENTIAL for: - Quasi-Newton methods (BFGS, L-BFGS) - Trust region algorithms - Second-order neural network training - Advanced machine learning optimization SERIES PLAYLIST: This is Part 4 in my Optimization Algorithms series: Part 1: Genetic Algorithm ➜ Part 2: Gradient Descent ➜ Part 3: Conjugate Gradient Descent ➜ Part 4: Newton's Method (this video) Part 5: Quasi-Newton Methods (BFGS) - Coming Soon! 💬 LET'S CONNECT: Questions? Drop them in the comments below! Follow me for more optimization content: 🔗 GitHub: 🔗 LinkedIn: / satyam-sangeet-a8a604119 🔗 Twitter: 💬 Personal Page: 🔔 SUBSCRIBE for the next video on Quasi-Newton Methods (BFGS/L-BFGS) - the workhorses of real-world machine learning! 👍 If you found this helpful, please LIKE and SHARE! --- #newtonsmwthod #machinelearningalgorithm #optimizationalgorithm #deeplearningmodels #datascience #mathematics #gradientdescent #algorithm #tutorial #Manim #python #ai #numericalmethods #computerscience #MathematicalOptimization #stem #education #programming #maths #learntocode