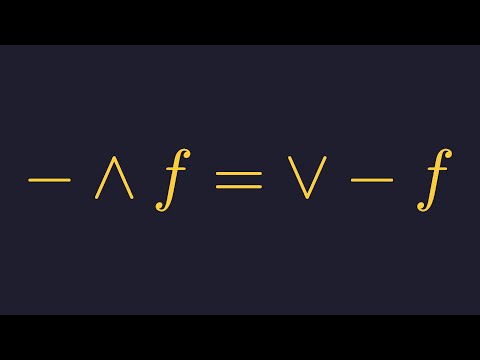No matter how hard we try to axiomatise mathematics, there will always be strong, independent propositions that don't need no proofs... but how do we *show* that a proposition can't be proven nor disproven? __________ Timestamps: 00:00 - Motivation(al) 01:14 - What is logical independence? 02:47 - An axiomatic foundation of "integers" 04:45 - A provable proposition 05:36 - An unprovable proposition 06:29 - An unprovable and undisprovable proposition 07:35 - The usual integers 08:35 - The undisprovability of the Freshman's Dream 10:08 - The big idea 10:41 - Thx 4 watching
- 34639Просмотров
- 1 год назадОпубликованоSheafification of G
(Provably) Unprovable and Undisprovable... How??
Похожее видео
Популярное
Потеряный снайпер
Грань правосудия 5
Universal effects
ПОТЕРЯННЫЙ СНАЙПЕР 3
Scar lion king face paint halloween makeup
КРАСНАЯ ГАДЮКА 3
poterianij snaiper 2 seria
184
патерений снайпер фқлм 2
макс и катя новогодний
Цена отказа 7-8 серии
ВОЛШЕБНАЯ КАРУСЕЛЬ
ну погоди 18 конец
Ликвидатор Среди Магов
Городской снаипер 8 серия
Грань правосудия 4сезон
5 серия
american pie college
Сезон охоты
Badalados assistimos 2022
Universal fanfare cover in low voice Luigi group
мультик
Безжалостный гений 3
ису или борьку
Грань правосудия 5
Universal effects
ПОТЕРЯННЫЙ СНАЙПЕР 3
Scar lion king face paint halloween makeup
КРАСНАЯ ГАДЮКА 3
poterianij snaiper 2 seria
184
патерений снайпер фқлм 2
макс и катя новогодний
Цена отказа 7-8 серии
ВОЛШЕБНАЯ КАРУСЕЛЬ
ну погоди 18 конец
Ликвидатор Среди Магов
Городской снаипер 8 серия
Грань правосудия 4сезон
5 серия
american pie college
Сезон охоты
Badalados assistimos 2022
Universal fanfare cover in low voice Luigi group
мультик
Безжалостный гений 3
ису или борьку
Новини