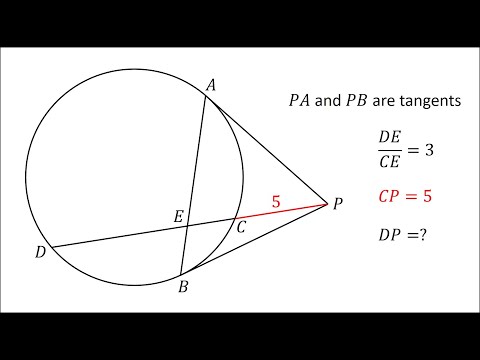
Can you find the ratio 𝑎:𝑏:𝑐 in this elegant circle geometry puzzle? In this problem, several circles with different radii are arranged inside a larger circle. The key idea is not to compare areas directly, but to first compare the radii using geometry. First, I construct a right triangle whose side lengths are the different radii of the circles. Then, I apply the Pythagorean theorem to find the ratio of the radii. Once the radii ratio is known, I compute the fraction of area formed by the four small and medium circles relative to the area of the large circle. ✨ This step-by-step approach turns a visually complex diagram into a clean and solvable geometry problem. 🎯 Perfect for: Kangaroo & Olympiad geometry preparation SAT and GCSE circle problems Students practicing geometric reasoning and symmetry Anyone who enjoys elegant math puzzles with a clever twist 👉 Try solving it yourself before watching the full explanation! What do you think the ratio a:b:c is? If you enjoy problems like this, don’t forget to like, subscribe, and share to support MathSpark. #Geometry #CircleGeometry #MathPuzzle #KangarooMath #OlympiadMath #PythagoreanTheorem #RadiiRatio #AreaRatio #VisualMath #ProblemSolving #MathSpark #ContestMath